機械学習-回帰分析ではどういったモデルを作成するのかが重要になってきます。
作成したモデルがどれほど正確なものなのか判断するのに「決定係数」を利用します。
この記事では「決定係数」がどういったものなのか、どう計算すればよいのかをサンプルコードを使い説明します。
以下に当てはまる項目がある方は参考にしてください。
- 回帰分析モデルの精度を確かめたい
- 機械学習について学びたい
- 機械学習の仕組みを知りたい
- 決定係数の求め方を知りたい
簡単にモデルを作成するサンプルコードを紹介しますが、作り方については『【機械学習の基本】値予測のやり方を解説|1次関数の傾きと切片を求める』を参考にしてください。
どういった考え方で、どう作るのか解説しています。
この記事ではまず、作成したモデルの精度を測るために利用する「決定係数」がどういったものなのか説明します。
概要を把握できたら、なぜそういった計算をするのか理解することができます。
すでに回帰分析について知識がある方は飛ばしてください。
そのあと、実際にサンプルコードを動かしながら、どう計算するのか説明していきます。
モデルの精度を測る「決定係数」とは
たとえば「y = ax + b」といった関数の「a:傾き」「b:切片」を割り出し、モデルを作成したとします。
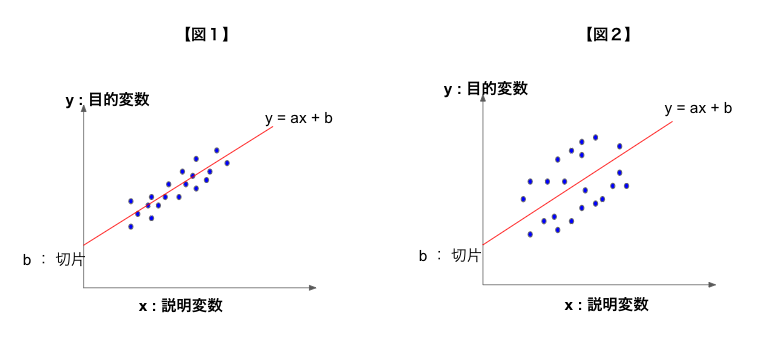
この図1、図2でもわかる通り、同じモデル(y = ax + b)が作成できたとしても、精度が違います。
図1の方が目的変数(y)に近いデータを取得できることがわかるでしょう。
図にするとなんとなくモデルの精度がわかりますが、数値化して正確に測りたいですよね。
そのときに使うのが「決定係数」です。
正確にいうと、「どのくらい分散を説明できているのか」を表す数値です。
分散については『【悪用厳禁】数字にダマされないデータ分析の基礎|平均、中央値、分散、標準偏差』にまとめています。
決定係数は0から1の間の数値となり、1に近いほど精度が高いものになります。
決定係数を割り出す変動について
決定係数を計算するには3つの変動を利用します。
- 全体変動
- 回帰変動
- 残差変動
全体変動
全体変動は「平均値ー実測値」で計算することができます。
実測値とはモデルを作成するために利用した元データになります。
実際のデータが平均からどの程度離れているのかを表します。
回帰変動
回帰変動は「平均値ー予測値」で計算することができます。
予測値は作成したモデルを利用して得られる値(y)です。
平均と回帰モデルにて予測したデータがどれだけ離れているのか表します。
残差変動
残差変動は「予測値ー実測値」で計算できます。
回帰モデルで予測したデータと実際のデータがどれだけ離れているのかを表しています。
決定係数を計算する
変動をまとめるとこのようになります。
- 全体変動:平均値 ー 実測値
- 回帰変動:平均値 ー 予測値
- 残差変動:予測値 ー 実測値
まとめると「全体変動 = 回帰変動 + 残差変動」となります。
決定係数は「回帰変動÷全体変動」で計算できます。
つまり全体変動のうちの回帰変動の割合が決定係数です。
どれだけ離れているかが重要なので、実際に計算するときは、それぞれの数値を平方(2乗)します。
サンプルコードを動かして計算する
Pythonのコードを動かしながら実際に決定係数を計算していきます。
まずは以下のコードを実行してモジュールを読み見込んでください。
import numpy as np
import pandas as pd
from pandas import DataFrame「NumPy」「Pandas」「DataFrame」については以下で説明しています。
・【NumPy入門】機械学習はここから始める|計算方法、配列の作り方、配列の変形
・【Pandas入門】機械学習の基礎知識 -効率的な学習法-|調べて実践できる
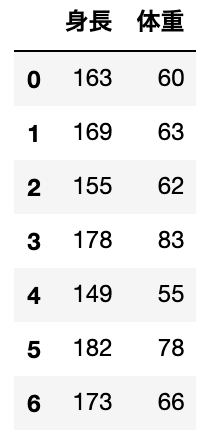
この記事では以下のデータを利用していきます。
data = DataFrame({
'身長' : [163, 169, 155, 178, 149, 182, 173],
'体重' : [60, 63, 62, 83, 55, 78, 66]
})
モデル作成
作成したデータを元に、身長から体重を予測するモデルを作成してみます。
# 平均
ave = np.mean(data)
# 相関係数
corr = data.corr()
# 標準偏差
tall_std, wight_std = np.std(data)
# 共分散:相関係数×標準偏差
cov = corr['身長']['体重'] * tall_std * wight_std
# 分散
tall_var, weight_var = np.var(data)
# 傾き
a = cov / tall_var
# 切片
b = ave['体重'] - (a * ave['身長'])モデルの作成については『【機械学習の基本】値予測のやり方を解説|1次関数の傾きと切片を求める』に詳細をまとめているので、確認してください。
(同じデータを使っています)
以下のデータを算出することができました。
- a(傾き) : 0.7252873563218389
- b(切片) : -54.408702791461394
モデルは「体重 = 0.7252873563218389 × 身長 – 54.408702791461394」となります。
変動を求める
モデルが作成できたところで、精度を測るための決定係数の材料となる変動を計算していきます。
data = data.rename(columns={'体重' : '体重(実測値)'})
# 予測値
dic = []
# 全体変動
all_fluc = []
# 回帰変動
reg_fluc = []
# 残差変動
diff_fluc = []
for i in range(0,len(data)):
# 予測値
i_dic = a * data['身長'][i] + b
dic.append(i_dic)
# 全体変動
i_all_fluc = (ave['体重'] - data['体重(実測値)'][i]) ** 2
all_fluc.append(i_all_fluc)
# 回帰変動
i_reg_fluc = (ave['体重'] - i_dic) ** 2
reg_fluc.append(i_reg_fluc)
# 残差変動
diff_fluc.append((data['体重(実測値)'][i] - i_dic) ** 2)
data['予測値'] = dic
data['全体変動'] = all_fluc
data['回帰変動'] = reg_fluc
data['残差変動'] = diff_fluc各種変動と実測値、予測値はこのようになりました。

「全体変動」「回帰変動」「残差変動」は数値の大きさを測るものなので、平方(2乗)してあります。
決定係数を求める
「全体変動」「回帰変動」「残差変動」を求めることができたので、決定係数を計算していきます。
決定係数は「全データの回帰変動の合計 ÷ 全データの全体変動の合計」で計算します。
data['回帰変動'].sum() / data['全体変動'].sum()決定係数は「0.7485033301106451」となりました。
まぁまぁ使えそうなモデルですね。
最後に
作成したモデルが利用可能なものなのか「決定係数」を利用して判断するようにしてください。
この記事ではモデルの精度を測る「決定係数」にフォーカスをあてて説明しましたが、『Udemy![]() 』を利用すれば、機械学習の一貫した学習を行うことができます。
』を利用すれば、機械学習の一貫した学習を行うことができます。
全世界で約3000万人が利用しており、講座の質も高いです。
現在セール中で1万円代の講座を1,000円代で受講することができます!
セール終了するともったいないので、いまのうちに買っておいたほうがお得です。
一回購入すると、ずっと、何回でも受けられるので、損はありません。
ぼくもこれまで10講座以上受講して満足できているので、是非使ってみてください。
最後まで読んでくださり、ありがとうございました!!!



コメント