機械学習には大きく3つの方法があります。
- 教師あり学習
- 教師なし学習
- 強化学習
この記事では教師なし学習の1つ「階層化クラスタリング」の6つの方法について説明していきます。

- 階層化クラスタリングの種類を知りたい
- グループ分類の方法を学びたい
- 機械学習のイメージを持ちたい
- 階層化クラスタリングのサンプルコードをみたい

階層化クラスタリングの6つの方法について、どう分類するのか説明していきますね。
実際にPythonを使って利用する方法も紹介していくので、手元で動かしながらイメージを深めていくとよいと思います。
まず階層化クラスタリングについて説明します。
どういったことができるのか概要を把握しておいてください。
その後、実際に6つの方法について説明していきます。
階層化クラスタリングについて
「階層化クラスタリング」は教師なし学習であるグループ分類の1つです。
なにか答えを求めるものではなく、分類してクラスター(まとまり)をつくることが目的です。
特徴として、事前にクラスター数を決めないことがあります。
事前にクラスター数を指定して、それに合わせて分類するのは「非階層化クラスタリング」を利用します。
簡単にまとめるといっても、基準によっていろいろなまとめ方があります。
機械学習では以下の6つの方法があります。
- 単連結法
- 完全連結法
- 群平均法
- ウォード法
- 重心法
- メディアン法
階層化クラスタリングの基本については『【機械学習の入門編】教師なし学習の基本 – グループ分類|階層化クラスタリング実践』を参考にしてください。
おおよそのイメージがつくようになります。
6つの手法説明 -サンプルコードあり-
「階層化クラスタリング」の6つの方法について、分類方法と実装方法を紹介していきます。
まずは以下のコードを実行して必要なモジュールの読み込み、サンプルデータの準備をしておいてください。
import numpy as np
import pandas as pd
from scipy.cluster.hierarchy import dendrogram, linkage
import pylab as plt
data = pd.DataFrame({'国語':[65,80,92,58,80,92,67,78,82,69],
'数学':[65,67,59,72,92,83,67,73,78,85]},
index=['Aさん','Bさん','Cさん','Dさん','Eさん','Fさん','Gさん','Hさん','Iさん','Jさん'])
name = ('Aさん','Bさん','Cさん','Dさん','Eさん','Fさん','Gさん','Hさん','Iさん','Jさん')
# 平均行の追加
ave_data = pd.Series(data.mean(), name='平均')
data.append(ave_data)ここでは10人の「国語」「数学」のテストデータから分類していきます。
テストデータはこのようになっています。
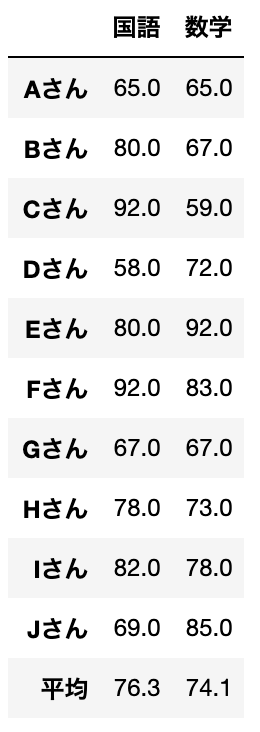
※最後の行に平均データをいれていますが、利用しないので、除いても大丈夫です。
表でみてもわかりずらいので、散布図を表示してみましょう。
plt.scatter(x=data['国語'], y=data['数学'])
plt.xlabel('国語')
plt.ylabel('数学')
plt.show()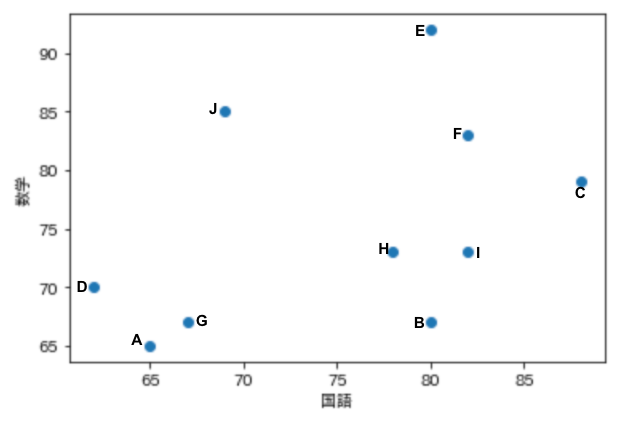
※各データの人名は手入力しています。
このデータを利用して、6つの手法を実行していきます。
階層化クラスタリングには「SciPy」の「linkage関数」を利用します。
単連結法
「最短距離法」とも呼ばれています。
分類に利用するクラスター間の距離は「もっとも近いデータ間の距離」を利用します。
分類比較するクラスター内のデータで一番近いもので算出します。
特徴としてはこれらがあります。
- 外れ値に弱い
- 帯状になりやすい
- 分類感度が低い
実際にクラスタリングを行って樹形図を表示してみましょう。
「linkage関数」の”method”引数に「single」を指定します。
result1 = linkage(data, method = 'single')
# 単連結法の樹形図
dendrogram(
result1,
leaf_rotation=90.,
leaf_font_size=14.,
labels=name)
plt.rcParams["font.family"] = "IPAexGothic"
plt.show()このような樹形図ができあがります。
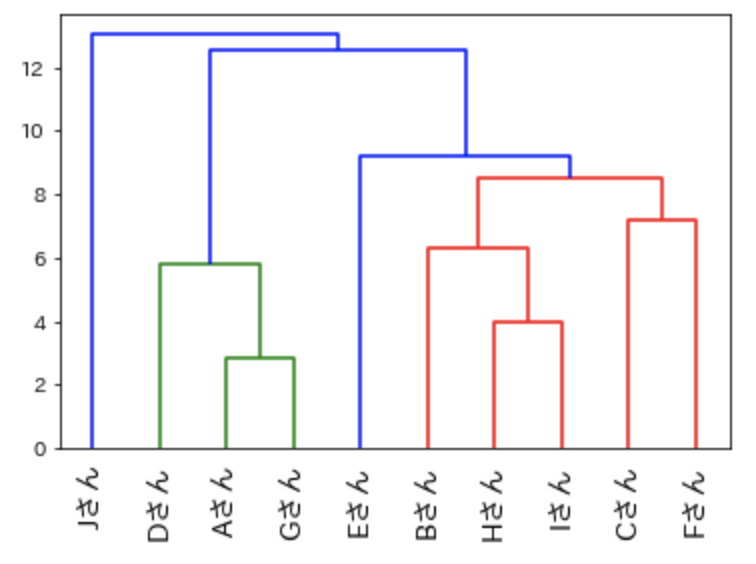
分類感度が低いため、あまり使われることがありませんが、計算が簡単なため、「linkage関数」のデフォルトとなっています。
完全連結法
「最長距離法」と呼ばれています。
「単連結法」と逆の分類方法になります。
分類に利用するクラスター間の距離は「もっとも遠いデータ間の距離」を利用します。
分類比較するクラスター内のデータで一番遠いもので算出します。
特徴としてはこれらがあります。
- 外れ値に弱い
- クラスター同士が離れる
- 分類感度は単連結法より良いが弱い
「linkage関数」の”method”引数に「complete」を指定します。
result2 = linkage(data, method = 'complete')
# 完全連結法の樹形図
dendrogram(
result2,
leaf_rotation=90.,
leaf_font_size=14.,
labels=name)
plt.rcParams["font.family"] = "IPAexGothic"
plt.show()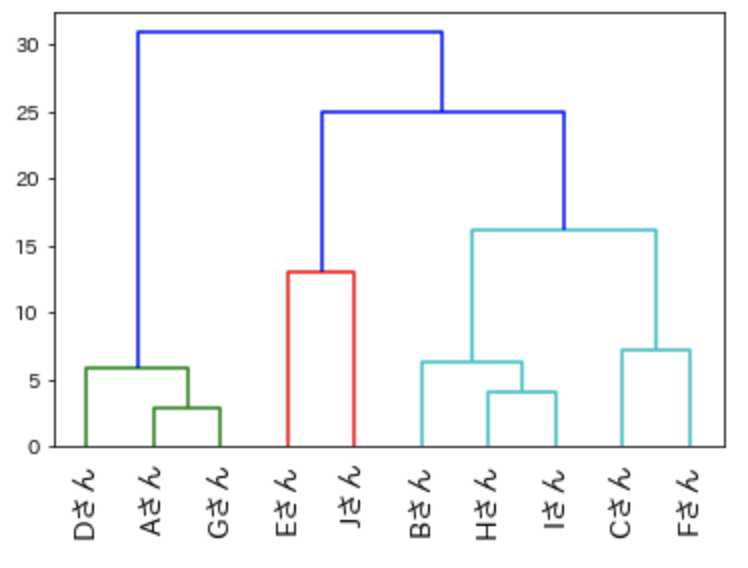
「単連結法」よりは分類感度が良いので、どちらかというとこちらを利用するほうがよいでしょう。
しかし、まだ分類感度は弱い方法になります。
群平均法
クラスター内のすべてのデータの距離の平均をクラスター間の距離とする方法です。
すべてのデータの距離を利用しているので、外れ値には強い特徴があります。
特徴をまとめると以下があります。
- 外れ値に強い
- 帯状になりにくい
- クラスター同士が離れにくい
「linkage関数」の”method”引数に「average」を指定します。
result3 = linkage(data, method = 'average')
# 群平均法の樹形図
dendrogram(
result3,
leaf_rotation=90.,
leaf_font_size=14.,
labels=name)
plt.rcParams["font.family"] = "IPAexGothic"
plt.show()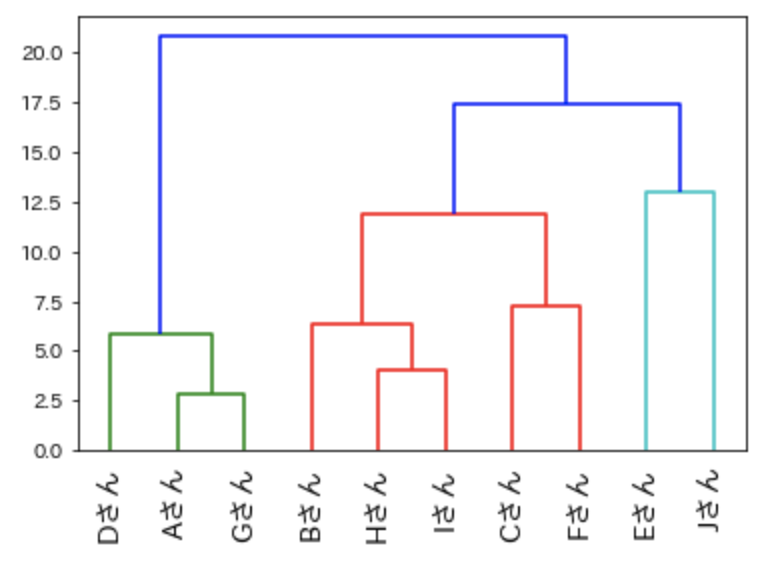
外れ値が多くある、大きい場合は「群平均法」を使ってみるとよいでしょう。
重心法
クラスター同士の重心の距離を利用します。
実際のデータの点を使うのではなく、クラスター内の中心からの距離を使う方法になります。
重心法は「類似性」を測るのに優れています。
「linkage関数」の”method”引数に「weighted」を指定します。
result4 = linkage(data, method = 'weighted')
# 重心法の樹形図
dendrogram(
result4,
leaf_rotation=90.,
leaf_font_size=14.,
labels=name)
plt.rcParams["font.family"] = "IPAexGothic"
plt.show()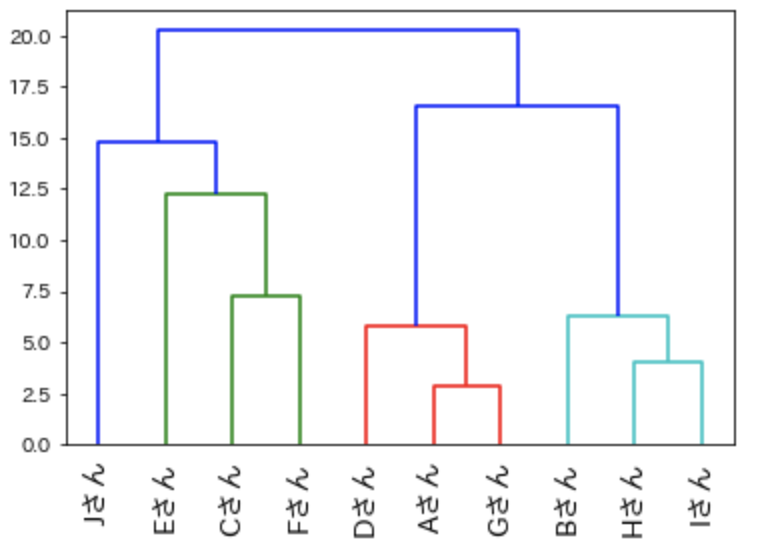
クラスター内の重心を利用するので、クラスター自体の類似性を比較する際に利用してください。
メディアン法
「重心法」と同じように重心からの距離を利用するものですが、データ数でクラスターに重みをつけて分類する方法です。
データ数が多く、類似性を測る場合に利用すると良いでしょう。
「linkage関数」の”method”引数に「centroid」を指定します。
result5 = linkage(data, method = 'centroid')
# メディアン法の樹形図
dendrogram(
result5,
leaf_rotation=90.,
leaf_font_size=14.,
labels=name)
plt.rcParams["font.family"] = "IPAexGothic"
plt.show()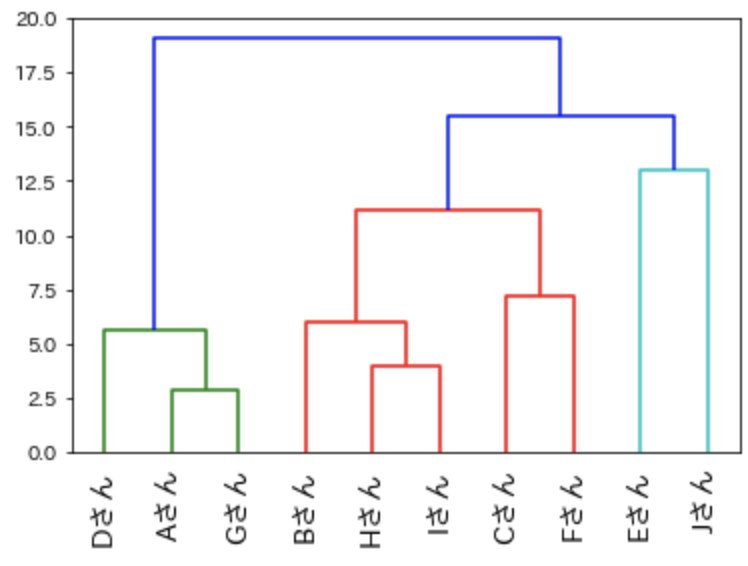
「重心法」より分類感度がよいので、どちらか利用することを迷った際は「メディアン法」を利用することをオススメします。
ウォード法
6つの方法の中でもっとも考え方がムズカシイものであり、もっともよく利用される方法になります。
距離を測るのに以下の要素の差を利用します。
- 既存のクラスターの重心
- クラスターをまとめたときの新しいクラスターの重心とクラスター内の前データの距離の2乗和
簡単にいうと、分類する前と後での重心からの距離の違いです。
「linkage関数」の”method”引数に「ward」を指定します。
result6 = linkage(data, method = 'ward')
# ウォード法の樹形図
dendrogram(
result6,
leaf_rotation=90.,
leaf_font_size=14.,
labels=name)
plt.rcParams["font.family"] = "IPAexGothic"
plt.show()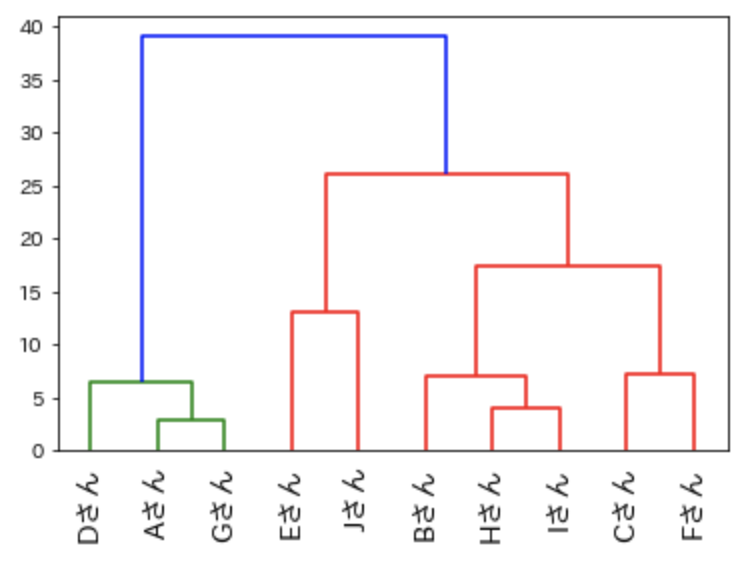
もっともよく利用されている手法ですが、外れ値には弱い方法です。
外れ値を重視した分類の場合は別の方法を利用しましょう。
最後に
「階層化クラスタリング」は機械学習のほんの一部であり、それだけで利用することはあまりありません。
その他の「教師あり学習」などと組み合わせて利用することが多いです。
独学で学習することもできますが、学ぶことが多いため、一貫した内容で学習を進めないと、必要以上に時間がかかってしまいます。。。
そこで、ぼくも利用している『Udemy』をオススメします。
全世界で3000万人が利用している実績もあり、10万以上の講座があるため、自分が求める講座を見つけることもできます。
本来1万円代の講座が現在セール中で「1,000円代」で購入できます!
安いうちに試しに受講して学習してみてはいかがでしょうか。
多くのことを学ぶ必要がありますが、楽しみながら学んでいきましょう。
最後まで読んでくださり、ありがとうございました!!!



コメント