【機械学習-回帰分析】t値を理解して利用することで回帰モデルの変数を説明する

これまで回帰分析でモデルを作成して、決定係数でモデルの精度を確かめてきました。

・【機械学習の基本】値予測のやり方を解説｜１次関数の傾きと切片を求める
・【機械学習-回帰分析】決定係数を求めてモデルの精度を確かめる｜サンプルプログラムあり

決定係数でモデルの精度を確かめても、説明変数(「y = ax + b」のx)がどれほど目的変数を説明できているのか確かめられていません。

そこで利用するのが「t値」です。

この記事ではt値について解説していきます。

以下に当てはまる項目がある方は参考にしてください。

回帰モデルの変数の精度を確認したい
t値ってどういうものか知りたい
t値の計算方法がわからない
機械学習の勉強をしたい

まずt値とはどういう数字なのか解説していきます。
数字の意味を理解することで、ちゃんと利用することができるようになるので、飛ばさずに読んでください。

そのあと、なるべく自分で計算してt値を求めていきます。
上から実行していけばt値を計算できるPythonのサンプルコードも紹介していくので、理解を深めるために利用してください。

t値について
サンプルコードで実装
最後に

t値について

「決定係数」はモデル自体の精度を測るのに対し、「t値」は説明変数がどの程度説明できるのかを表した数値です。

モデルを作るデータに意味がある差があるかどうかを表しているのです。
簡単にいうと、説明変数が使えるかどうかを判断できる数値です。

回帰分析には１つの説明変数を利用する「単回帰分析」と複数の説明変数を利用する「重回帰分析」があります。

この記事では「単回帰分析」を実施します。
「y = ax + b」の「a」と「b」を求めて回帰モデルを作成します。

「a」と「b」を求めるのに使った説明変数(x)がどのくらい目的変数(y)を説明できているのかを判断していきます。

「t値」を考える要素

「t値」を計算するには以下の要素を理解する必要があります。

帰無仮説
有意水準

それぞれについて説明していきます。
統計学でも使うワードなので、しっかりと理解してください。

帰無仮説

「帰無仮説」は説明変数が関係ないことを仮説しています。
「関係ないこと」ということに注意してください。

つまり帰無仮説が採択されたら、説明変数が関係ないものであることを表します。

逆に帰無仮説が採択されない(棄却)場合は説明変数が関係している、つまりはモデルが使える可能性が高いことを表しています。

有意水準

「有意水準」は帰無仮説の判断基準となる確率です。

一般的に5%(0.05)が使われます。

つまり、帰無仮説(説明変数が使えない)が起こる可能性が５％ということです。

逆に考えると、９５％説明変数が関係あるということを表しています。

「t値」の判断基準

「t値」を求めることができたら、どう説明変数が関係ある(帰無仮説が間違っている)かどうか判断できるのか説明していきます。

ズバリ「２以上かどうか」が判断基準となります。

2未満：帰無仮説があっている可能性が高い
2以上：帰無仮説が間違っている可能性が高い

「t値」が２以上であれば、説明変数は説明できているということになり、モデルに使用できる可能性が高いことになります。

計算方法

t値は「係数 ÷ 標準誤差」で求めることができます。

係数は「y = ax + b」の「a」のことです。

標準誤差は「(残差平方和 ÷ 自由度 ÷ 説明変数の偏差平方和)の平方根」で求めることができます。

自由度とは「データの個数 – 変数の個数(x,y)」のことです。

イメージしづらいかと思うので、実際のサンプルコードをみていき、理解を深めていきましょう。

サンプルコードで実装

「t値」を求めるサンプルコード(Python)を紹介します。
上から順番に実行していけば、動くようになっているので、実際に手元で試してください。

まずはモジュールを読み込みます。

import numpy as np
import pandas as pd
from pandas import DataFrame

「NumPy」「Pandas」「DataFrame」については以下で説明しています。
・【NumPy入門】機械学習はここから始める｜計算方法、配列の作り方、配列の変形
・【Pandas入門】機械学習の基礎知識 -効率的な学習法-｜調べて実践できる

実際に利用するデータを作成します。

data = DataFrame({
    '身長' : [163, 169, 155, 178, 149, 182, 173],
    '体重' : [60, 63, 62, 83, 55, 78, 66]
})

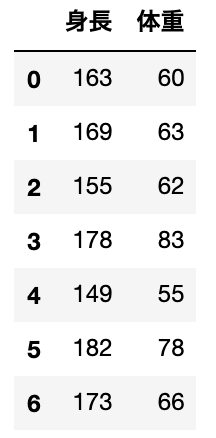
このデータでモデルを作成してみます。

# 平均
ave = np.mean(data)

# 相関係数
corr = data.corr()

# 標準偏差
tall_std, wight_std = np.std(data)

# 共分散：相関係数×標準偏差
cov = corr['身長']['体重'] * tall_std * wight_std

# 分散
tall_var, weight_var = np.var(data)

# 傾き
a = cov / tall_var

# 切片
b = ave['体重'] - (a * ave['身長'])

次は「t値」を計算するのに利用する「残差変動」を割り出してみます。

# 残差変動
diff_fluc = []

for i in range(0,len(data)):
    # 予測値
    i_dic = a * data['身長'][i] + b
    # 残差変動
    diff_fluc.append((data['体重'][i] - i_dic) ** 2)
    
data['残差変動'] = diff_fluc

残差変動はこのようになりました。

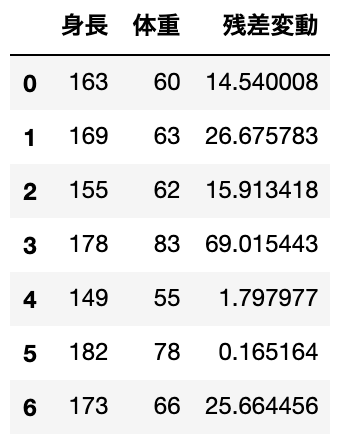
では実際に「t値」を求めていきましょう。
t値は「係数 ÷ 標準誤差」で計算できるので、まず標準誤差を計算してから、t値を割り出しています。

標準誤差は「(残差平方和 ÷ 自由度 ÷ 説明変数の偏差平方和)の平方根」で求めています。

# t値 = 係数(a) ÷ 標準誤差

# 残差平方和
d_sum = data['残差変動'].sum()

# 自由度
free = len(data) - 2

# 説明変数の偏差平方和
x_sum = 0
for i in range(0,len(data)):
    x_sum += (data["身長"][i]-ave['身長'])**2

# 標準誤差
norm_diff = np.sqrt(d_sum / free / x_sum)
    
# t値
t_value = a / norm_diff

t値は「3.857587192759244」となりました

２以上なので、説明変数は説明できるものである可能性が高いです。

t値はこのように計算することができます。