機械学習には「教師あり学習」「教師なし学習」「強化学習」の3つがあります。
それぞれの違いについては『意外と知らない機械学習の基礎知識・種類|データサイエンティストのスキルを身につける』を参考にしてください。
この記事では「教師なし学習」である「グループ分類」の「非階層クラスタリング」について説明していきます。
以下に当てはまる方は参考にしてください。
- データを分類したい
- 非階層クラスタリングのやり方を知りたい
- k平均法(k-means法)の使い方がわからない
- 機械学習でどういうことができるのか知りたい
まず「階層クラスタリング」と「非階層クラスタリング」の違いについて説明します。
つぎに「非階層クラスタリング」の計算方法を説明していきます。
どういう計算で分類しているのかわかれば、自分で使えるもの、使えないものを判別することができます。
かならず理解しておきましょう。
最後にPythonのコードを紹介しながら、サンプルデータを分類してみます。
「階層クラスタリング」と「非階層クラスタリング」の違い

事前にいっておくと、「階層クラスタリング」「非階層クラスタリング」どちらか一方だけ使うケースは少ないです。
このような使い方をすることが多いからです。
- 階層クラスタリングで自動的に分類したものを、非階層クラスタリングで検証
- 非階層クラスタリングで決まった数に分類して、階層クラスタリングで検証
それでは違いについて説明していきます。
階層クラスタリング
データを下から上に積み上げていき、分類していく方法になります。
データを1つずつ積み上げていき、クラスター(まとまり)を作っていきます。
大きな特徴として、事前の準備なく分類していくということになります。
計算方法やサンプルプログラムは『【機械学習の入門編】教師なし学習の基本 – グループ分類|階層化クラスタリング実践』を参考にしてください。
非階層クラスタリング
クラスター数(グループ数)を事前に決めた上で分類していくことが特徴です。
グループが事前にわかっている場合などに利用するとよいでしょう。
使い勝手としては「非階層クラスタリング」のほうがよいケースが多そうな気がします。
実際、どのように分類するのか見ていきましょう。
【計算方法】k平均法(k-means法)
クラスター(グループ)数を指定して分類していくのに用いられるのが「k平均法(k-means法)」です。
ここでいう「k」がクラスター数となります。
分類の考え方として、クラスターそれぞれのデータから中心点までの平均を使用します。
実際に分類する4つのステップを説明します。
ステップ1)ランダムにデータを分類する
指定したクラスター数でデータをランダムに分類します。
この時点では適当に分類しているので、意味のない分類となっています。
これが正確に分類していくための土台となります。
※後ほど問題点と解決方法について説明します。
ステップ2)中心点の計算
各クラスターの中心点を計算します。
最終的には、各データと中心点の距離を最小にすることができたら、分類できている状態となります。
グループ分類はこの最適な中心点を探していく作業になるのです。
まずはランダムに作ったクラスターの中心点を割り出してみます。
ステップ3)データ分類に見直し
あるデータにフォーカスしてみると、ランダムに分類しているので、より近い中心点(クラスター)があるはずです。
そのより近いクラスターに分類し直します。
ステップ4)中心点の再計算、再分類を繰り返す
データの分類を見直すと中心点もズレていくので、再度計算し直しが必要になります。
中心点を再計算して、データの再分類を繰り返していくことでグループ分けが完了するのです。
問題点
この方法ですべて分類できるかと思いますが、欠点があります。。。
最初のランダムなデータ分類で中心点が近くなってしまった場合、分類ができません。
そこで有効なのが「k-means++法」です。
最初のデータの選び方が重要になってくるので、中心を初期化することで、分類できるようにする方法になります。
サンプル実装(k-means++)
問題点を改善した「k-means++法」を使って、10人のテスト結果を2つに分類してみます。
まずは必要なモジュール、ライブラリを読み込みます。
import pandas as pd
from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as pltグループ分類に「scikit-learn」を使用します。
図で表示するために「matplotlib」を利用していますが、必要ない場合は読み込む必要ありません。
分類する10人のテストデータを用意します。
data = pd.DataFrame({'国語':[65,80,88,62,80,82,67,78,82,69],
'数学':[65,67,79,70,92,83,67,73,73,85]},
index=['Aさん','Bさん','Cさん','Dさん','Eさん','Fさん','Gさん','Hさん','Iさん','Jさん'])
name = ('Aさん','Bさん','Cさん','Dさん','Eさん','Fさん','Gさん','Hさん','Iさん','Jさん')データはこのようになっています。
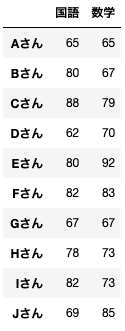
わかりやすいよう以下を実行して表にしてみましょう。
plt.scatter(x=data['国語'], y=data['数学'])
plt.xlabel('国語')
plt.ylabel('数学')
plt.show()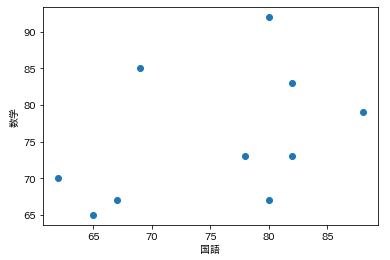
このデータを分類してみやすくしてみましょう。
#kmeansのモデル生成
kmeans = KMeans(n_clusters=2, init='k-means++', random_state=0)
#モデルにデータを当てはめる
y_kmeans = kmeans.fit_predict(data)
# グラフの作成
plt.scatter(x=data['国語'], y=data['数学'], c=y_kmeans, s=20, cmap='viridis')
#中心点を求める
centers = kmeans.cluster_centers_
#中心点をプロット
plt.scatter(centers[:, 0], centers[:, 1], c='black', s=100, alpha=0.3)
plt.show()このような表が取得できます。
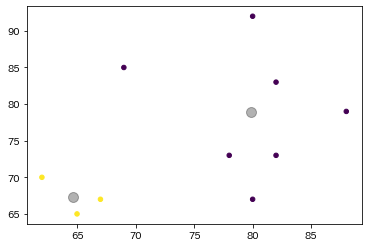
グループごとに点の色が異なり、中心点(大きな点)を表示しています。
ここではデータ数が少なくてわかりやすいですが、データ数が多いときに有効な手法なので、試したいデータで利用してみてください。
最後に
紹介した「非階層クラスタリング」は機械学習のうちの1つにすぎません。
これだけでは何か答えを出すことができないため、その他の手法と組み合わせることで初めて意味のあるものとなります。
ぼくも利用している『Udemy ![]() 』は現在1万円以上の講座が1,000円代で受講することができます。
』は現在1万円以上の講座が1,000円代で受講することができます。
中には20時間以上の講座もあり、機械学習などの一貫した内容の講座を受けることができます。
たとえば、このようなものがあります(2020/10/27現在)。
- 【世界で18万人が受講】実践 Python データサイエンス : 1,560円
- 【徹底的に解説!】人工知能
- 機械学習エンジニア養成講座(初級編~統計学から数字認識まで~):1,500円
- AIパーフェクトマスター講座 -Google Colaboratoryで隅々まで学ぶ実用的な人工知能/機械学習-:1,500円
オンライン講座で買い切りなので、電車の中などで受講可能なので、空き時間で勉強したい方は是非利用してください!
最後まで読んでくださり、ありがとうございました!!!



コメント