データのグループ分類には「階層クラスタリング」と「非階層クラスタリング」があります。
非階層クラスタリングではクラスター数を指定して、それに合わせてデータを分類していきます。
この記事では「k-means法」で分類する際に「エルボー法」を使って、最適なクラスター数の求め方を紹介します。
以下に当てはまる項目がある方は是非最後まで読んでください。

- k-meansで指定するクラスタ数が決めれない
- クラスタリングの方法を知りたい
- 機械学習でなにができるのか知りたい
- 実装方法がわからない
- エルボー法って何?
まずクラスタリングの概要を説明します。
機械学習の基本となる知識なので、機械学習についてこれから学ぶ方は念入りに読んでください。
次にエルボー法でクラスター数を決める流れを紹介します。
最後にサンプルデータを使って、クラスター数を決めるところから、割り出したクラスター数を使ってデータを分類するサンプルコードを紹介します。
クラスタリング概要
クラスタリングとは「データを特定の情報から分類していく」作業のことです。
分類のやり方にもいくつかあります。
1つ目は「階層化クラスタリング」です。
これはデータをなんの条件もなく、下から上に積み上げていくような分類方法になります。
階層化クラスタリングについては↓↓↓をご覧ください。
もう1つはこの記事でも紹介する「非階層クラスタリング」です。
分類を始める前に、いくつのグループに分類するのか指定する方法です。
計算方法などについては↓↓↓を参考にしてください。
このように機械学習には様々なやり方が、広く深くあります!
独学で学ぶこともできますが、一貫した内容の講座を受けたほうが正確に、かつ早く身に着けることができます。
ぼくがいつも利用している『Udemy』というサービスを簡単に紹介します。
- 10万以上の講座があるので、身につけたいものにピッタリのものがある
- セール中で1,000円代で受講できるものが多い
- 20時間にも及ぶ講座もある
- オンライン講座なので、電車の中でも受講できる
- 買い切りなので、何回も受けれる
セール中の間は圧倒的に安いので、いまのうちに試してみてください!
Udemyの利用方法、使った感想は↓↓↓をご覧になってください。
クラスター数を決める

「エルボー法」を利用して、分類するデータの最適なクラスター数を求めていきます。
k-means法の場合、クラスターの中心点と各データの距離が近くなることが目的となります。
もっとも最適な分類は、中心点と各データの距離を小さくしながら、なるべく多くのまとまりを作ることです。
この距離には「残差平方和」を使います。
具体的には中心点とデータの距離の2乗した数値を利用するのです。
(2乗することで符号の関係がなくなる)
流れはこのようになります。
- 複数のクラスター数を指定したk-meansのモデルを作る
- それぞれの2乗誤差を算出
- クラスター数が増えても変化がなくなった数が最適なクラスター数といえる
簡単にいうと、いくつものモデルで距離を測ってみて、誤差が落ち着き出したところが最適なものであるということになります。
実装
10人のテストの点数のデータを「k-means」を使って分類していきます。
その前に「エルボー法」を使ってクラスター数を決めていくので、参考にしてください。
まずは以下を実行してモジュール、ライブラリを読み込みます。
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
import pylab as plt次に10人のサンプルデータを準備します。
data = pd.DataFrame({'国語':[65,80,88,62,80,82,67,78,82,69],
'数学':[65,67,79,70,92,83,67,73,73,85]},
index=['Aさん','Bさん','Cさん','Dさん','Eさん','Fさん','Gさん','Hさん','Iさん','Jさん'])
name = ('Aさん','Bさん','Cさん','Dさん','Eさん','Fさん','Gさん','Hさん','Iさん','Jさん')見やすくするとこのようになります。
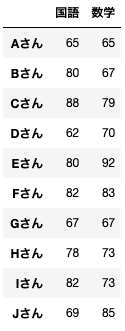
分類する前に図で表示してわかりやすくしてみます。
分類後も同じように表示するので、比較してみてください。
plt.scatter(x=data['国語'], y=data['数学'])
plt.xlabel('国語')
plt.ylabel('数学')
plt.show()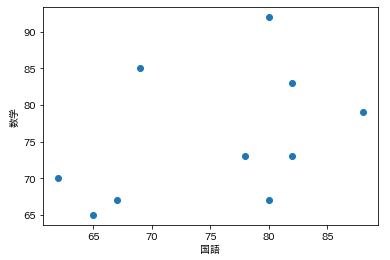
それでは実際にクラスター数を決めていきましょう!
以下のように、データ数の分だけモデルを作成して距離を検証していきます。
sse = []
for i in range(1, len(data.index)):
km = KMeans(n_clusters=i,
init='k-means++',
n_init=10,
max_iter=300,
random_state=0)
km.fit(data)
inertia_= np.round(km.inertia_,3)
sse.append(inertia_)
plt.plot(range(1, len(data.index)),sse,marker='o')
plt.xlabel('クラスタ数')
plt.ylabel('誤差')
plt.show()このような図が表示されます。
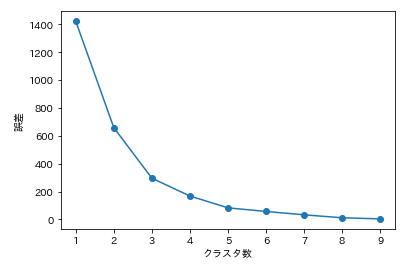
k-meansの「inertia_」は二乗誤差を取得しています。
青い線を肩から腕に見立てたときのヒジの箇所が最適なクラスター数となることから「エルボー法」と呼ばれています。
この場合はクラスター数は「3」となります。
それでは3つに分類してみましょう。
#kmeansのモデル生成
kmeans = KMeans(n_clusters=3, init='k-means++', random_state=0)
#モデルにデータを当てはめる
y_kmeans = kmeans.fit_predict(data)
# グラフの作成
plt.scatter(x=data['国語'], y=data['数学'], c=y_kmeans, s=20, cmap='viridis')
#中心点を求める
centers = kmeans.cluster_centers_
#中心点をプロット
plt.scatter(centers[:, 0], centers[:, 1], c='black', s=100, alpha=0.3)
plt.show()このようになります。
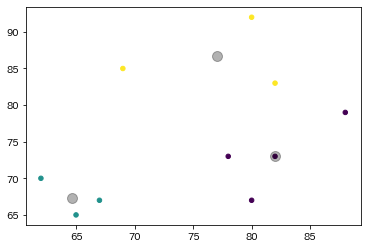
目視してもわかりやすいようになっています。
是非データを変えて試してみてください。
最後に
データを正しく分類することができたら、「教師あり学習」などの未来を予測する精度を高めることができます。
この記事では理解・利用が容易な「エルボー法」でのクラスター数の求め方、「k-means」を利用したデータの分類を紹介しました。
機械学習は学ぶことの範囲が広く、かつ奥が深いです。
紹介しているのはほんの一部です。
自分が欲しい情報、分析したい情報から学ぶことを決めてください。
最後まで読んでくださり、ありがとうございました!!!






コメント