データを分析するには、データを分析しやすい状態にする必要があります。
そのための1つがデータのクラスタリング(分類)です。
この記事では「シルエット法」を用いてデータを分類する方法を説明します。
以下に当てはまる項目がある方は参考にしてください。
- 機械学習に興味がある
- 分析する前にデータを分類したい
- データの分類方法を知りたい
- 分析する実際のコードを知りたい
最初にデータ分類の種類を説明します。
「シルエット法」がどの段階で用いるものなのか理解してもらえたらと思います。
次に分類数(クラスター数)の決め方を説明します。
シルエット法の考え方、計算方法を説明するので、理屈を把握してください。
最後は実装コードを紹介します。
まず、クラスター数を指定して分類したあとに、「シルエット法」を使って分析してみます。
最終的に最適なクラスターを求めていきます。
データ分類の種類

データの分類、つまりクラスタリングには大きく2つあります。
- 階層クラスタリング
- 非階層クラスタリング
階層クラスタリングはデータを順番に下から上に積み上げていく方法です。
分類数の指定なしに、順番に分類していくことが特徴です。
計算方法や実装方法などの詳細は『【機械学習の入門編】教師なし学習の基本 – グループ分類|階層化クラスタリング実践』を参考にしてください。
一方、非階層クラスタリングは分類する前にグループ(クラスター)数を指定して、分類していく方法です。
これから説明していく「シルエット法」はクラスター数を割り出す際に利用するので、非階層クラスタリングを実行する前に利用するものになります。
非階層クラスタリングについては『【機械学習-グループ分類】非階層クラスタリングの概要と実装方法』を参考にしてください。
これからのクラスタリングは機械学習でいう「教師なし学習」の1つです。
機械学習には数多くの考え方、知識が必要になります。
一貫した内容で学んでいくには『Udemy』を利用することをオススメします。
ぼくも機械学習の勉強で数多くの講座を受講させてもらいました!
全部で10万以上の講座があるため、特化したものから、全体像を捉えるためなど様々な要望を叶えてくれます。
現在秋セール中で1万円代の講座がなんと「1,500円から」受講できます!
試すにはちょうどよいくらいの金額なので、セール中の内に買ってみてください。
買い切り型なので、1度買ってしまえば追加費用は発生しません。
クラスター数の決め方
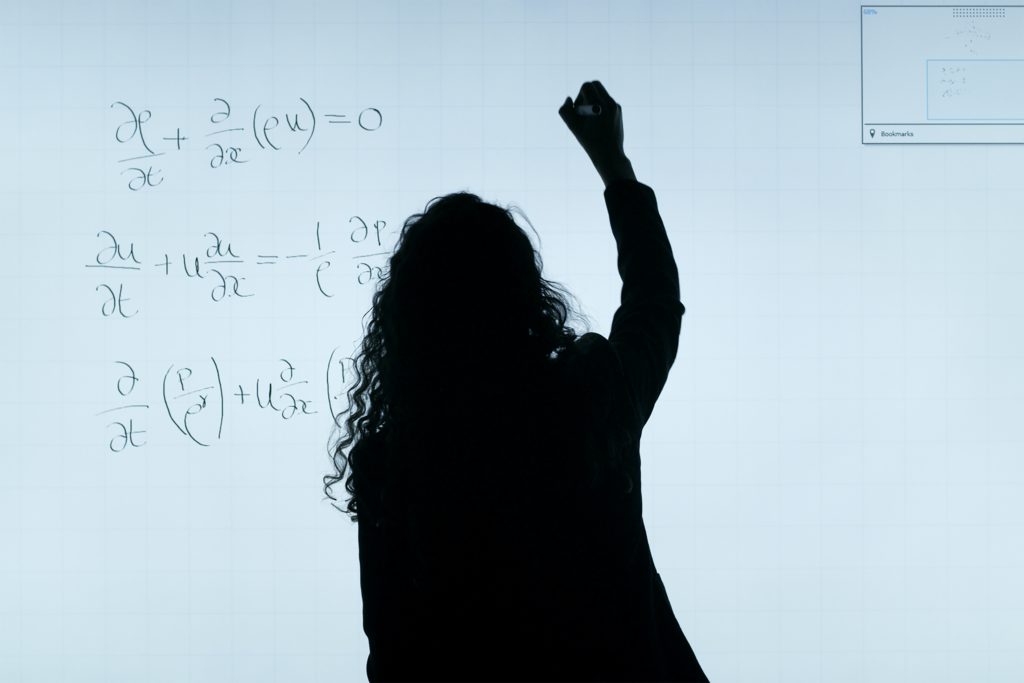
非階層クラスタリングを行う場合、クラスター数を指定する必要があります。
分類したい数が決まっていたらよいのですが、最適な分析を行いたい場合はどのようにクラスター数を決めたらよいのでしょうか。
1つは「エルボー法」があります。
全部のデータと各クラスターの中心点との距離を使用する方法です。
計算方法、実装方法などの詳細は『【機械学習-クラスタリング】k-meansを使用したクラスタリングのクラスター数の決め方〜エルボー法〜』を参考にしてください。
しかし、外れ値があるという欠点があります。
クラスター内のデータがどれほど密集しているのかはわからないのです。
そこで、この記事では2つ目の方法「シルエット法」を説明していきます。
クラスター内のデータの密集度を測る方法です。
k-means法以外にも利用できるので、便利な考え方になります。
シルエット法-計算の流れ-
シルエット法の計算の流れをみて概要を理解しましょう。
1)凝縮度を求める
2)乖離度を求める
3)シルエット係数を求める
「凝縮度」はあるデータと同じクラスタ内のすべてのデータとの平均距離を割り出します。
あるデータの「近さ」が割り出せるのです。
「乖離度」はあるデータと属していない中で一番近いクラスター内との平均距離を割り出します。
あるデータの「遠さ」を割り出すものになります。
「シルエット係数」は「凝縮度から乖離度を引いたもの」を「凝縮度、乖離度の大きい方」で割ることで計算できます。
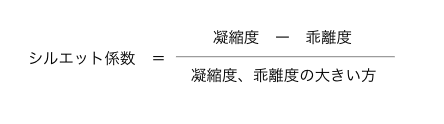
凝縮度が0に近いほど理想的なクラス分類といえることは理解しやすいと思います。
クラスター内のデータが近いからです。
↑の式に当てはめると、シルエット係数が1に近いほど距離が近いもの、つまり理想的なクラス分類と言えるのです。
【実装】シルエット法の利用
これからは実際にPythonのコードを実行しながら説明していきます。
まずは以下のコードを実行してモジュール、ライブラリを読み込みましょう。
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
import pylab as plt
from matplotlib import cm
from sklearn.metrics import silhouette_samples今回は10人のテスト(国語、数学)の点数から10人を分類してみます。
以下を実行してテストデータを作成しておきます。
data = pd.DataFrame({'国語':[65,80,88,62,80,82,67,78,82,69],
'数学':[65,67,79,70,92,83,67,73,73,85]},
index=['Aさん','Bさん','Cさん','Dさん','Eさん','Fさん','Gさん','Hさん','Iさん','Jさん'])
name = ('Aさん','Bさん','Cさん','Dさん','Eさん','Fさん','Gさん','Hさん','Iさん','Jさん')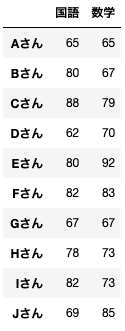
以下を実行するとグラフ上で見やすくすることができます。
plt.scatter(x=data['国語'], y=data['数学'])
plt.xlabel('国語')
plt.ylabel('数学')
plt.show()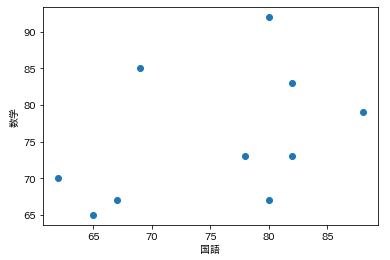
クラスター数を指定して結果を分析してみる
まず「k-means法」を使用して分類します。
その後にシルエット係数を計算して、分析するためにグラフ化しています。
都度コメントでわかりやすく説明しているので確認しながら読んでください。
km = KMeans(n_clusters=4,
init='k-means++',
n_init=10,
max_iter=300,
random_state=0)
# クラスタ分類→[2, 1, 0, 2, 3, 0, 2, 1, 1, 3]
y_km = km.fit_predict(data)
# クラスタの重複をなくす→[0, 1, 2, 3]
cluster_labels = np.unique(y_km)
# 配列の数:指定したクラスタ数→4
n_clusters = cluster_labels.shape[0]
#シルエット係数を計算(引数:サンプルデータ, クラスター番号、ユークリッド距離でシルエット係数計算)
silhouette_vals = silhouette_samples(data,y_km,metric='euclidean')
y_ax_lower, y_ax_upper = 0,0
yticks = []
for i,c in enumerate(cluster_labels):
c_silhouette_vals = silhouette_vals[y_km==c]
c_silhouette_vals.sort()
# サンプルの個数を足していく
y_ax_upper +=len(c_silhouette_vals)
# グラフ表示の色を作成
color=cm.jet(float(i)/n_clusters)
# 棒グラフを作成
plt.barh(range(y_ax_lower,y_ax_upper),
c_silhouette_vals,
height=1.0,
edgecolor='none',
color=color
)
# クラスタラベルの表示位置
yticks.append((y_ax_lower+y_ax_upper)/2.)
# 底辺の値に棒の幅を足していく
y_ax_lower += len(c_silhouette_vals)
#平均の位置に線を引く
silhouette_avg=np.mean(silhouette_vals)
plt.axvline(silhouette_avg,color="red",linestyle="--")
plt.ylabel("Cluster")
plt.xlabel("Silhouette coefficient")コードの半分近くがグラフ表示のものです。
実行するとこのようなグラフが取得できます。
※わかりやすくするために説明文を加えています
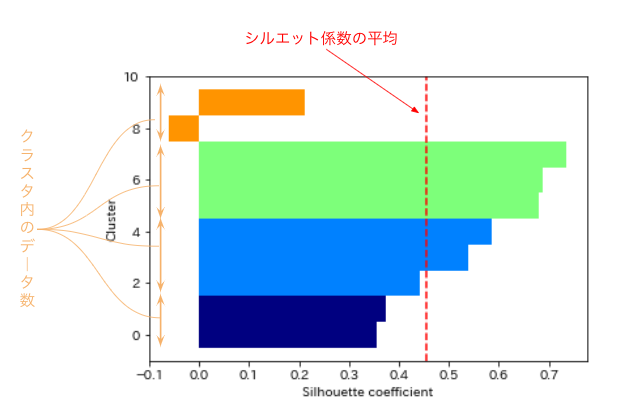
色ごとにクラスターが表示されています。
横棒(クラスター)の縦幅がクラスター内のデータ数になっています。
また横軸が「シルエット係数」で縦の点線がクラスター平均のシルエット係数です。
見る時のポイントは以下の3つです。
- クラスター内のデータ数がどのクラスターでも同じくらい
- どのクラスター内でもクラスター係数の平均を超えている
- クラスター係数の平均が1に近いほど正確に分類できている
各クラスター内のデータ数は同じくらいであるほど理想的であるといえます。
またシルエット係数の平均は「1」に近ければ良い形で分類できていると言えます。
最適なクラスター数を割り出す
クラスター数の分析ができるようになりました。
あとは複数のクラスター数を自動的に作成して分析していけばよいのです。
つまり、繰り返し様々なクラスター数で分類してみて、もっともよいクラスター数を決めるのです。
ここでは以下の2点より最適なクラスター数を割り出しています。
- クラスター内のデータ数の差分が全体の2割以下
- シルエット係数平均がもっとも高いもの
では実際にクラスター数を割り出すコードを見ていきましょう。
class_data_list = []
result_class_num = 0
# 2〜データ個数の9割りまでクラスタ数を指定する
loop_num = int(len(data.index) * 0.9)
for class_num in range(2, loop_num):
# クラスタ分類
km = KMeans(n_clusters=class_num,
init='k-means++',
n_init=10,
max_iter=300,
random_state=0)
y_km = km.fit_predict(data)
cluster_labels = np.unique(y_km)
# 配列の数
n_clusters = cluster_labels.shape[0]
#シルエット係数を計算
silhouette_vals = silhouette_samples(data,y_km,metric='euclidean')
# クラスタ内のデータ数
sil=[]
for i,c in enumerate(cluster_labels):
c_silhouette_vals=silhouette_vals[y_km==c]
sil.append(len(c_silhouette_vals))
# クラスタ内のデータ数の差がデータ数の2割以下であれば分割できたとみなす
data_diff = int(len(data.index) * 0.2)
data_diff_flg = max(sil)-min(sil) < data_diff
# クラスタ内のシルエット係数平均値
ave_silhouette_vals = np.average(silhouette_vals)
class_data_list.append({'class_num':class_num, 'data_diff':data_diff_flg, 'ave':ave_silhouette_vals})
max_ave = 0
for class_data in class_data_list:
if class_data['data_diff'] and (max_ave < class_data['ave']):
max_ave = class_data['ave']
result_class_num = class_data['class_num']
print(result_class_num)やっていることはシンプルです。
「2」から「データ個数の9割」までクラスター数を繰り返し分類して、「データ幅」「シルエット係数」を割り出しています。
ちなみに最適なクラスター数は「3」になりました!
最後に
機械学習を進めていくうえで、思うようなデータが集まらないことが多いです。
その場合は、データが正確に分類して、意味のあるものになっていない可能性があります。
実際に分析していく前にデータがまとまったものになっているのか確認するようにしてください。
わからないところ、間違っているところがありましたら『お問い合わせ』もしくは『Twitter』よりご連絡ください。
また分析してほしいものがありましたら、抽象的でもよいのでご連絡ください。
分析できるのか確認したものを含めて回答いたします。
※先着1名限り無料
最後まで読んでくださり、ありがとうございました!!!



コメント