こんにちは、こがたです。
機械学習には答えを導き出す「教師あり学習」があります。
実際の値を予測する方法もあれば、データの属性(クラス)を割り出すこともできます。
この記事では機械学習による「クラス識別」を説明します。
同じような方は参考にしてください。

- クラス識別を学習中
- 機械学習のできることを知りたい
- Pythonで機械学習を実装したい
- データをクラス分けして識別したい
まずはクラス識別とはどういうものか、種類と考え方を説明します。
なんとなくでよいので、クラス識別がどう行われているのか理解してください。
次にPythonでサンプルデータをクラス識別していきます。
具体的な利用方法を抑えてください。
クラス識別の考え方と種類

クラス識別は機械学習の中でも「教師あり学習」にあたります。
つまり、実際のデータから答えを予測するものになります。
教師あり学習には、値を予測する回帰分析というものもあります。
詳細は『【機械学習の基本】値予測のやり方を解説|1次関数の傾きと切片を求める』をご覧になってください。
一方、「クラス識別」はデータがどのクラス(カテゴリ)に分類されるのかを割り出してくれるものになります。
機械学習の種類(教師あり学習など)については『意外と知らない機械学習の基礎知識・種類|データサイエンティストのスキルを身につける』を参考にしてください。
クラス識別の種類・方法
クラス識別はこのようにデータを線で区切って分類します。
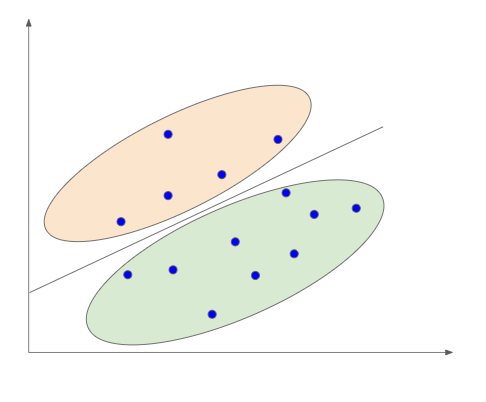
この区切っている線を「決定境界」と呼びます。
決定境界とデータが離れているほど、正確にクラス分けができていることになります。
つまりクラス識別では「データと最大の距離をとった決定境界を引くこと」が目的となります。
この記事で紹介するカーネル法ではクラス分けの失敗、損失の大きさにhinge関数を使用します。
他の関数を指定することもできますが、hinge関数が利用するのが一般的です。

ん?急にムズカシイよぉ〜

そうですよね、、、
簡単にいうと、決定境界から大きく離れたデータは使用せず、計算量を減らすやり方です。
それではクラス識別の種類(カーネル法)について説明していきます。
この記事では代表的な3つを紹介します。
- 線形分離
- 非線形分離:ガウスカーネル
- 非線形分離:多項カーネル
線形分離とは決定境界が直線となるものです。
「y = ax + b」という式になります。
一方、非線形分類は決定境界は曲線となります。
次元数(クラス識別の判断材料)を増やすことで曲線となっていくのです。
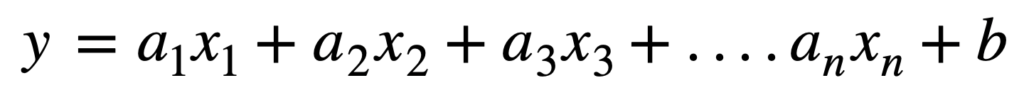
データを説明する特徴を抽出しやすくなることがメリットです。
反面、計算量が増えるというデメリットがあります。
非線形分離のイメージはこのようになります。
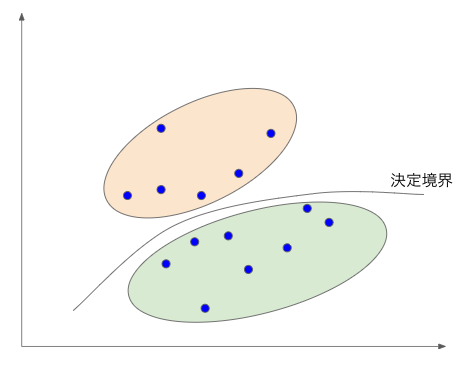
ガウスカーネルは2つのデータの差を分散で割ることで特徴量を抽出する方法です。
識別する際に分散数を指定することが特徴です。
多項カーネルは次元数を指定して正接曲線で特徴空間を作る方法です。
離散特徴でよく利用されるものになります。
実践(サンプルコード)
10人の国語と数学の点数をクラス識別していきます。
まず利用するモジュール・ライブラリを読み込みます。
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
import pylab as plt
import sklearn
from sklearn import svm, metrics, preprocessing, model_selection
from mlxtend.plotting import plot_decision_regions
from sklearn.svm import LinearSVC利用するデータ(10人の点数)を準備します。
# データ
data = pd.DataFrame({'国語':[65,80,88,62,80,82,67,78,82,69],
'数学':[65,67,79,70,92,83,67,73,73,85]},
index=['Aさん','Bさん','Cさん','Dさん','Eさん','Fさん','Gさん','Hさん','Iさん','Jさん'])
name = ('Aさん','Bさん','Cさん','Dさん','Eさん','Fさん','Gさん','Hさん','Iさん','Jさん')
# クラスタリング
km = KMeans(n_clusters=3,
init='k-means++',
n_init=10,
max_iter=300,
random_state=0)
y_kmeans = km.fit_predict(data)
data['class'] = y_kmeansここでは目的となるクラスをk-menas法を用いて割り当てています。
詳細は『【機械学習-グループ分類】非階層クラスタリングの概要と実装方法』をご覧になってください。
分類したデータはこのようになります。
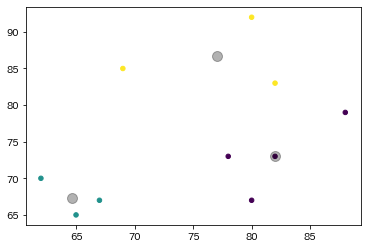
クラス識別を行っていきます。
X=data[["国語","数学"]]
#正規化 (平均0 標準偏差1)
sc=preprocessing.StandardScaler()
sc.fit(X)
X_std=sc.transform(X)
clf = LinearSVC()
#モデルを作成する
#線形分離:カーネル ヒンジ関数(誤差関数)の二乗誤差を最小化
clf.result1=svm.LinearSVC(C=1.0)
#ガウスカーネル
clf.result2=svm.SVC(C=1.0, gamma=0.1, kernel='rbf')
#3次元多項式カーネル
clf.result3=svm.SVC(C=1.0, kernel='poly',degree=3)
clf.result1.fit(X_std, data['class'])
clf.result2.fit(X_std, data['class'])
clf.result3.fit(X_std, data['class'])クラス識別と変数はこのようになっています。
- result1:線形分離
- result2:非線形分離(ガウスカーネル)
- result3:非線形分離(多項カーネル)
ここではガウスカーネルの誤差を0.1、多項カーネルの次元数を3としています。
決定境界を見やすくするために図にしてみます。
X_test_plot=np.vstack(X_std)
test_label_plot=np.hstack(data['class'])
plt.figure(figsize=(12,12))
plt.subplot(221)
plot_decision_regions(X_test_plot, test_label_plot, clf=clf.result1, res=0.01, legend=2)
plt.subplot(222)
plot_decision_regions(X_test_plot, test_label_plot, clf=clf.result2, res=0.01, legend=2)
plt.subplot(223)
plot_decision_regions(X_test_plot, test_label_plot, clf=clf.result3, res=0.01, legend=2)
plt.show()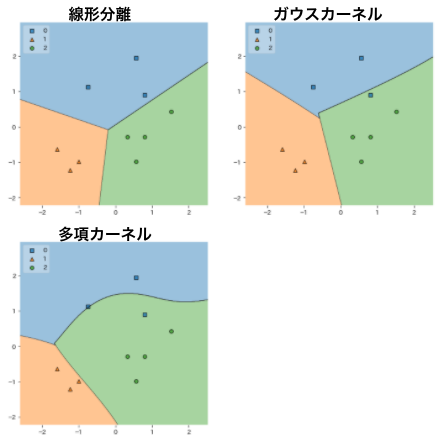
このように全データがクラス内のどこに位置しているのかが一目でわかります。
全データで識別してきました。
テストデータと検証データに分けて確認する方法も紹介します。
X=data[["国語","数学"]]
#正規化 (平均0 標準偏差1)
sc=preprocessing.StandardScaler()
sc.fit(X)
X_std=sc.transform(X)
clf = LinearSVC()
#モデルを作成する
#線形分離:カーネル ヒンジ関数(誤差関数)の二乗誤差を最小化
clf.result1=svm.LinearSVC(C=1.0)
#ガウスカーネル
clf.result2=svm.SVC(C=1.0, gamma=0.1, kernel='rbf')
#3次元多項式カーネル
clf.result3=svm.SVC(C=1.0, kernel='poly',degree=3)
#3割をテストデータに使用
X_train, X_test, train_label, test_label=model_selection.train_test_split(X_std, data['class'], test_size=0.3)
clf.result1.fit(X_train, train_label)
clf.result2.fit(X_train, train_label)
clf.result3.fit(X_train, train_label)「train_test_split」関数を利用して3割のデータをテストデータとして使用するように分類しています。
これを図にしてみます。
X_train_plot=np.vstack(X_train)
train_label_plot=np.hstack(train_label)
X_test_plot=np.vstack(X_test)
test_label_plot=np.hstack(test_label)
plt.figure(figsize=(12,12))
plt.subplot(221)
plot_decision_regions(X_test_plot, test_label_plot, clf=clf.result1, res=0.01, legend=2)
plt.subplot(222)
plot_decision_regions(X_test_plot, test_label_plot, clf=clf.result2, res=0.01, legend=2)
plt.subplot(223)
plot_decision_regions(X_test_plot, test_label_plot, clf=clf.result3, res=0.01, legend=2)
plt.show()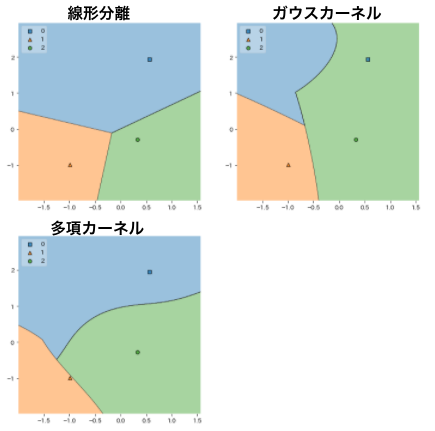
3割、つまり3つのデータでテストされていることがわかります。
ランダムでテストデータを取得するので、実行するたびに結果は変わります。
最後に
「クラス識別」はデータをカテゴライズするのに利用できます。
ただ単体で利用することは少なく、分析の過程として利用することが多いです。
機械学習には多くの手法があり、広く学んで初めて利用できるものなので、一貫した内容で学ぶことが重要です。
そこでPythonの基礎から機械学習、さらにはスクレイピングまでPythonに関することを網羅した講座を紹介します。
それは『PyQ』です!!
講座内容はこれらがあります。
- Python言語
- 設計方法
- Webサイト(Django)
- データ収集(スクレイピング)
- データ分析
- 機械学習
- 統計
Pythonでできることが全て網羅されています!
月額3,040円と月額8,130円のプランがあります。
これだけのことが学べてこの金額は他にはないので、是非利用してみてください。
最後まで読んでくださり、ありがとうございました!!!



コメント