機械学習には「教師あり学習」「教師なし学習」「強化学習」の3つがあります。
この記事では「教師あり学習」の「回帰分析」について説明していきます。
以下に当てはまる方は参考にしてください。
- 機械学習について勉強したい
- 回帰分析を行いたい
- 回帰分析での注意点を知りたい
- 実装コードをみてみたい
まずは回帰分析とはどういうもので、どんなことができるのか説明します。
なにか分析したいことがある方は「回帰分析」で実現できるのか確認してください。
次に回帰分析を行う上で、何を意識したらよいのか説明します。
教師データを集める際や使い物になるのか把握するために必須の内容となっているので、確認しておいてください。
最後にPythonのモジュール「statsmodels」を使って回帰分析を行う方法を紹介します。
サンプルデータの箇所を置き換えて分析したいデータを分析してください。
回帰分析とは

回帰分析をわかりやすく説明すると、大量のデータから「y = ax + b」の傾き(a)と切片(b)を割り出すことです。
回帰分析ではy、a、xのことをこのように呼びます。
- y : 目的変数
- a : 回帰変数
- x : 説明変数
回帰係数(a)と切片(b)を割り出すことができたら、任意の説明変数(x)から目的変数(y)を予測できるようになります。
このように1つの回帰係数、説明変数で説明できるものを「単回帰モデル(分析)」と呼びます。
より詳しい考え方や計算方法は『【機械学習の基本】値予測のやり方を解説|1次関数の傾きと切片を求める』にまとめてあります。
一方、複数の回帰係数、説明変数で説明できるものは「重回帰モデル(分析)」と呼ばれています。
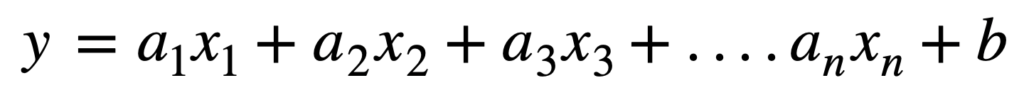
このように複数の回帰係数、説明変数の組み合わせでモデルを説明するものになります。
回帰分析で意識すること

単回帰分析と重回帰分析を比べると、複数の変数で説明(多角的に分析)できる重回帰モデルのほうが優れているようにみえます。
しかし以下の大きなデメリットがあります。
- 複雑になる
- 予測性能が落ちる
複雑になることで計算量が増えてしまいます。
さらに説明変数が増えることで、関係が増えて1つ1つの関係性が薄れて予測性能が落ちる可能性があります。
そのため、説明変数はなるべく少なく説明できるモデルを作ることを意識しましょう!
実際に説明変数を減らしていくときに利用するもの(相関関係、多重共線性)を紹介します。
相関関係 〜t値を利用〜
「t値」は説明変数がどの程度モデルを説明できているかを表す数値です。
具体的には「t値」が2以上であれば採用できる変数と判断できます。
2未満であれば、モデルで求めたものからデータが離れており利用できないことを表します。
各説明変数の「t値」が2以上なのか未満なのかで、利用できるかどうか見極めましょう。
「t値」の考え方、計算方法は『【機械学習-回帰分析】t値を理解して利用することで回帰モデルの変数を説明する』を参考にしてください。
多重共線性
「複数の説明変数が同じことを説明していないかどうか」という考え方になります。
深い関係があるものであっても、同じことを別の変数が説明できる場合、必要ありません。
同じことを説明しているかどうかは「必ずどちらかの説明変数に当てはまり、同時に当てはまることがない」かどうかで確認してください。
当てはまる説明変数がある場合は一方を削除してください。
たとえば「男性」という説明変数と「女性」という説明変数があったとします。
この場合、必ずどちらかに当てはまり、かつ同時に当てはまることがないので「性別」という説明変数にまとめます。
教師なし学習のグループ分類を使用する方法があります。
詳細は『【機械学習の入門編】教師なし学習の基本 – グループ分類|階層化クラスタリング実践』で紹介しているので参考にしてください。
サンプルデータで実践 -statsmodelsを利用-
実際にPythonのモジュール「statsmodels」を使って、サンプルデータからモデルを作成していきましょう。
まずは以下のコードを実行して必要なモジュールを読み込みます。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from pandas import DataFrame
import statsmodels.api as sm「jupyter notebook」を利用する場合は「% matplotlib inline」も実行しておいてください。
サンプルデータを作成していきます。
# サンプルデータ
data = DataFrame({
'年齢' : [20, 12, 32, 28, 15, 18, 13, 10, 22, 24],
'身長' : [166, 142, 169, 168, 152, 162, 149, 138, 164, 168],
'体重' : [66, 42, 73, 65, 51, 60, 45, 38, 60, 68],
'鼻の高さ' : [2.0, 1.8, 1.9, 1.8, 2.2, 2.0, 1.9, 2.0, 1.8, 1.9]
})ここでは「年齢」を目的変数(y)として、「身長」「体重」「鼻の高さ」を説明変数(x)として作成してみます。
以下を実行して回帰モデルを作成します。
# 説明変数:身長、体重、鼻の高さ
X = data.loc[:, ['身長', '体重', '鼻の高さ']].values
# 目的変数:年齢
Y = data['年齢'].values
# 回帰モデル作成
model = sm.OLS(Y, sm.add_constant(X))
# 結果
result = model.fit()説明変数は「X」で指定しているので、削除して実行すれば新しいモデルを作成することができます。
以下を実行して結果を表示してみましょう。
# 結果の表示
result.summary()以下のように表示されます。
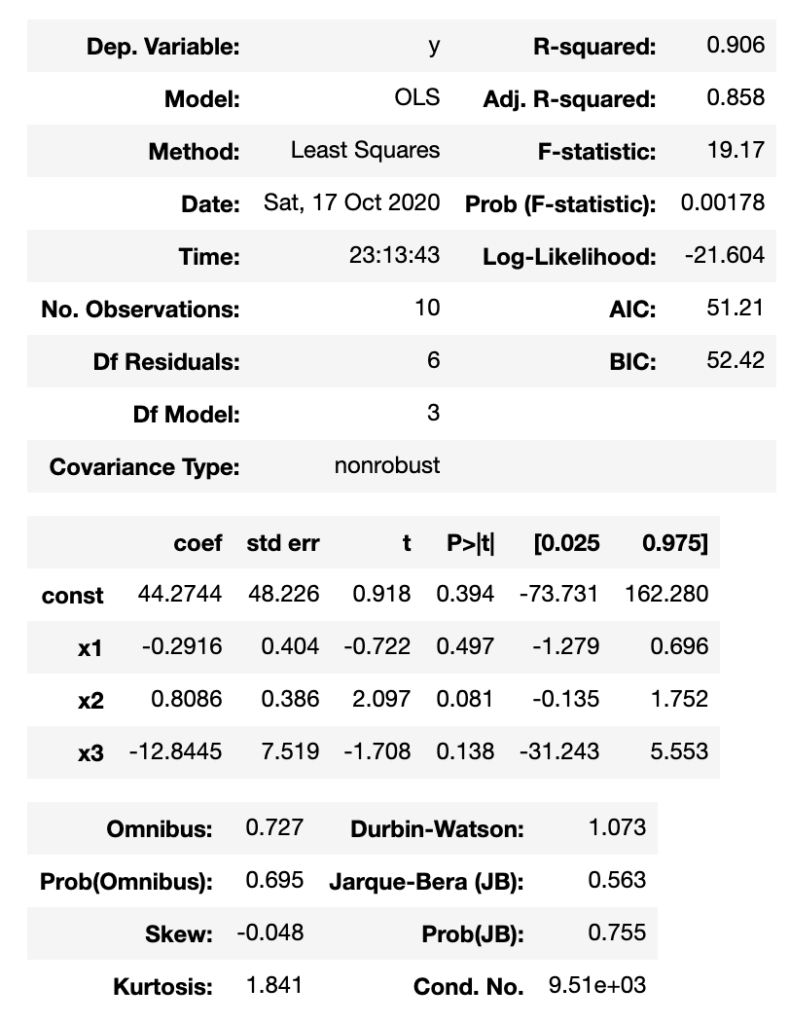
「x1」「x2」「x3」それぞれが「身長」「体重」「鼻の高さ」を表しています。
「coef」がそれぞれの回帰係数(a)を表しています。
「const : coef」が切片(b)の数値となります。
「t」列がt値を表しており、このデータからだと「年齢」と関係がある変数はt値が2以上である「体重」のみとみることができます。
最後に
回帰モデルとはどういったもので、どう考えて実装してけばよいか理解いただけましたでしょうか。
この記事で紹介した内容は、ほんの一部であり基本となるものです。
もっと複雑な使い方もあります。
時間をかければ独学で習得することもできますが、学ぶことが多く、都度調べながら進めていくのはムズカシイです。
そこでぼくも利用している『Udemy ![]() 』を紹介します。
』を紹介します。
全世界で約3000万人が利用しており、約10万もの講座があります。
20時間以上の講座が現在セール中で1,000円代で受講することができます!
試しに利用してみる金額としては高くないと思うので、学びたい内容を探して利用してみてください。
最後まで読んでくださり、ありがとうございました!!!



コメント